在我们的自然生活中有各种各样的数据,例如各个国家的人口、GDP、国土面积,甚至是视频网站的播放量、元素半衰期等,这些数据的首位数可能是 1、2、3、4、5、6、7、8、9,通常人们会以为每个数字打头的概率都相同,但实际上,科学家本福特等人发现:数字 1 打头的概率超过 30%。
我们先来看一下维基百科对本福特定律(Benford's law)的定义:
一堆从实际生活得出的数据中,以 1 为首位数字的数的出现概率约为总数的三成,是接近直觉得出的期望值 1/9 的 3 倍。越大的数,以它为首的数出现的概率就越低。
我们再来看一下数学上的定义:
本福特定律说明在X进位制中,以数n起头的数出现的概率为 logb(n+1)−logb(n)。有关数学证明,我不是相关专家,我就不再这里跟大家阐述了,有兴趣的小伙伴可以查看 show notes 中的链接。
P(D = d) = Log10(1+1/d)

2020年美国大选选票的统计: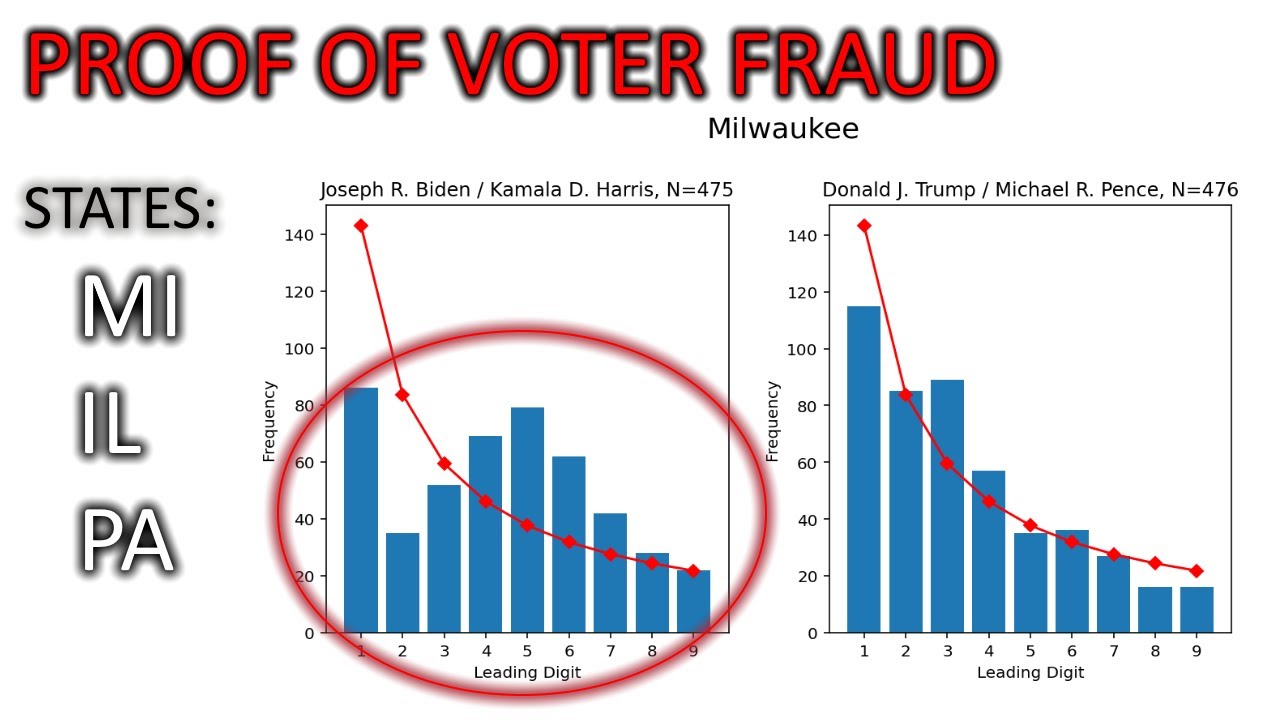
🔗 相关链接
- 如何判断一些数据是否造假呢?本福特定律
- 推特网民指控拜登选票数严重偏离“本福特定律”,啥情况?
- 为什么拜登的选票不符合本福特定律
- github.com
- 淘宝“双11”2684亿销售额造假了吗?用本福特定律检验一下
- 本福特定律的一个证明
- Benford's Law - Princeton University
📝 联系我
欢迎你给我发邮件,我的邮箱是 hi@gopod.fm ,也欢迎你加入来听呗 | GoPod.FM 听友群。



 7
7 0
0